Day 1 - 22nd August 2011

Day 1 22nd August 2011.
I am very excited today; it is my first lesson of a new module.  Not that I am very good at
Math. To let you know my grades for Math is F9. Not that I did not like Maths.  I just couldn’t understand what my teacher taught me.  She would say this is this and don’t ask why?  Many years ago we were not encouraged to question.  We did just as we were told. To question means to be disobedient.

I enjoy every minute of your lesson today.  Mainly because I could understand all you
taught and I could see that I can get the answer correct.  So it also boosts my morale and 

that’s why I wanted the lesson to go on and on and then I realize, "Wow! so fast it is ten o’clock.

Lesson 1 - The Name Game.      

B	A	N	H	A	R
1	2	3	4	5	6
11	10	9	8	7
	12	13	14	15	16
21	20	19	18	17
	22	23	24	25	26
31	30	29	28	27

I diligently followed the method up to six rows of numbers until I could see a pattern.  I found it rather amazing that I came up with the answer looking at the ending pattern.  WA LAH! I got a peg for this.  Motivation for me to look for other patterns, maybe I can get another Peg. Then amazingly my classmate came up with another method of doing it, like 99-6=93 then 93 divided by 5=18 remaining 3. 
Then I came up with another solution that is to look at 1, 11, and 21 till we reach 91 and then count forward to 99.

After trying a few names, the class came up with the pattern that is:-

6 letters multiple of 10

5 letters multiple of 8

7 letters multiple of 12

8 letters multiple of 14 and so on.

Today I also learned a few terminologies and have learned to use them in the correct context.

Cardinal numbers that is, 1, 2, 3, 4, 5, etc is used to count people, buses, cars, etc.

Ordinal numbers - first, second, third. Ordinal numbers are then divided into two terms; that is position in respect to time and position in respect to space. E.g. of a respect 
to time is: -Who is the third person from the finishing line.

I am also guilty of telling my students," Who came in third?" but now I know that this is wrong. I should say, "Who is third from the finishing line?" when we are using picture for the children to see. If it is a real race and you see them running than you can ask the children, "Who will come in third."

Nominal numbers:- they are just numbers that labels things e.g. Bus No. 14.  Frankly speaking, I had never heard of this phrase before this.

.A unit of measurement and A unit of proportion.

It was brought to my attention things that we are commonly guilty of doing in class, which is using object that are not of the same. I would always ask the children to count things that are not the same because I thought counting is just saying 1.2.3.4.5.6.7.8.9.10. So now, I tell my teachers that they should use objects that are identical if not, they are not good examples.

 (Lesson 2) Ten Frame

I have not taught using a ten frame before. 

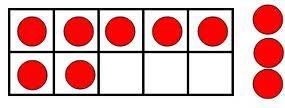
But I think it is a very effective tool when teaching Math. 
A ten-frame is considered an effective tool to teach all number relationships. 
For instance, teachers might add seven counters in a ten-frame and ask young children to subitize the quantity. If most of them are successful at the subitizing task, 
teachers might continue to encourage them to think of different interpretations of seven by presenting various arrangements For instance, seven can be easily understood in several ways, such as five and two, four and three, and three less than ten. I have learned that the ten frame can be used as an assessment tool for one to one correspondence and also for skip counting 5, 10, etc.  We assume that all children must have addition and subtraction fact.

I learned that children needs four prerequisite that is 

1) ability to classify must be there before they can count.  
2) The child must have the ability to do rote counting if he cannot count.
3) one to one correspondence, 
4) and the child needs to know that the last number represent the answer.

(Lesson 3)- The obedient Cards       

Another WOW factor in today’s lessons was the obedient cards. This is where we spell out numbers e.g. O...N...E... (one) and so on.  I tried it during assembly and all the children thought it was  magic.
This is how I arranged the number.  I had to lay out the cards on the table to arrange it in this way.

   
Lesson 4 – Add up

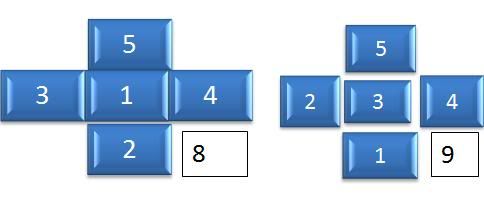
Using Numbers 1,2,3,4,5.

Using odd number in the middle, we came to the conclusion that by adding the first, second and last numbers gave us the number 8. For the second solution, we had 3 multiply by 3  and
we came up with the answer 9.  If we used the middle number as 5 we come up with the sum 10 and this pattern is the last two numbers added to the first number. That is 5 + 4+1=10

LESSON 5

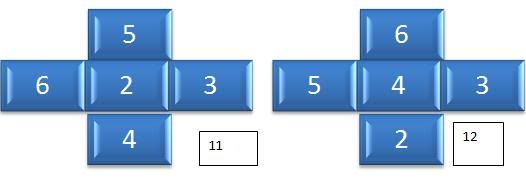
Using 23456

We came to a conclusion that if we were to add one more number, the total increases by one number that is 11, 12, and 13.
The same goes for this pattern. We add 2+3+6 (i.e. first second and last) to get 11
The second sum is middle number 4 multiply by 3 will give us 12. 
And if we did add one more to get 13 we must add the last two numbers that is 5+6+2 = 13.

Adding up- not very difficult if the numbers are small but when challenged by Mr, Yeap 72,73,74,75,76. 
I was like how to. Then I saw a pattern. Easy Lah! We also recognize that two even numbers can never equal an odd number. Two odd numbers always equal an even number.

In conclusion, a pattern is a sequence.  The sequence has a rule. A pattern has a rule.

To become a teacher of Mathematics, we must be persistent, have a positive attitude, readiness for change and have a reflective disposition.

We need to problem solve, need to reason and prove, communicate and make connection and representation and all of this we did in today’s lesson.

A very interesting lesson and it was all in a stress free environment where it doesn’t matter 
whether we got it right or wrong.  But I learned.  Listening to my classmate explanation,  
the understanding became easier. I believe more important are classroom environments in 
which children are encouraged to freely share their thinking about number and quantity with others. When all of the above come together, students usually surprise us with their depth of understanding.

Looking forward to tomorrow’s lesson.